点击下载PDF版

数据结构 第二章 算法分析.pdf

前言：

这份笔记，是我在学习数据结构过程中记下的笔记，并未完全遵循专业课的既定顺序与讲授逻辑。

于数据结构而言，这门学科从无捷径可走 —— 若想真正学懂吃透，核心唯有 “多练、多敲”。在此必须坦诚：我并不认同所谓的 “四件套速通课”，这类课程往往只能带你浅尝皮毛，难以触及知识的核心与本质。

如果你想要紧跟课堂进度，那么匹配课程的幻灯片会是更直接的参考（当然，前提是你能沉下心去研读）。不过市面上多数数据结构相关的书籍与幻灯片，存在一个共性问题：伪代码占比过高。若盲目照着这些伪代码直接编写，最终能成功运行的概率恐怕不足 10%。

正因如此，若你不嫌弃这份笔记的随性与朴实，我十分欢迎你将其作为学习参考。希望这些基于我个人实践的记录，能帮你更轻松地理解数据结构的逻辑，辅助你的学习之路。实现代码分为C语言描述与C++语言描述，各位按需获取。

最后说下这份笔记的使用建议：文中并未设置严格的章节划分，你大可以像读小说一样轻松浏览。唯独遇到具体的代码实现部分时，建议你停下脚步 —— 先完整读懂代码逻辑，再关掉笔记，试着独立敲写出属于自己的版本。唯有亲手实践，才能将知识真正内化为自己的能力。

By：ItsJiale

2025.10.1

第二章 算法分析

算法（Algorithms）+数据结构（Data Structures）=程序（Programs）

算法要满足的5个重要特性

有穷性

确定性

可行性

输入

输出

评价算法优劣的基本标准

正确性

可读性

健壮性

高效性

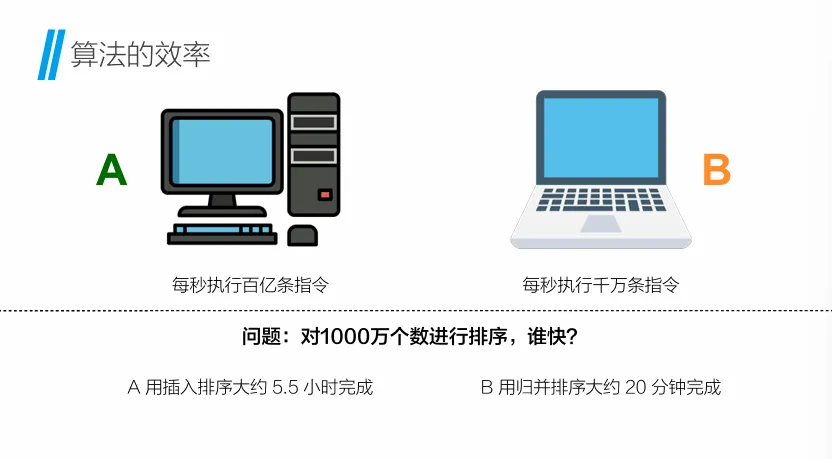
时间复杂度

也称渐近时间复杂度，T(n) = O(f(n)) 随着问题规模 n 的增大，算法执行时间和增长率和 f(n) 增长率成正比

程序运行的总时间主要和两点有关：1.执行每条语句的耗时 2.每条语句的执行频率

语句频度跟机器本身硬件有关

计算时间复杂度

若 f(n)=a_mn^m + a_m-1n^m-1 + … + a₁n +a₀ 是⼀个m次多项式，则 T(n)=O(n^m) 在计算算法时间复杂度时，可以忽略所有低次幂和最高次幂的系数，这样可以简化算法分析，也体现出了增长率的含义。

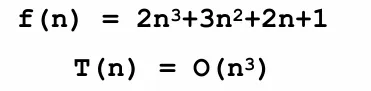
因为不是严格的数学计算，所以看最高次项即可

最好时间复杂度：算法在最好情况下的时间复杂度。

最坏时间复杂度：算法在最坏情况下的时间复杂度。

平均时间复杂度：算法在所有可能的情况下，按照输入实例以等概率出现时，算法计量的加权平均值。

对算法时间复杂度的度量，通常只讨论算法在最坏情况下的时间复杂度， 即分析在最坏情况下，算法执行时间的上界。

这里不提供时间复杂度求解的练习：一是代码太多难排版，二是讲解太难排版，三是自己动动笔更容易理解

空间复杂度

空间复杂度主要用来描述某个算法对应的程序想在计算机上执行，除了用来 存储代码和输入数据的内存空间外，还需要额外的空间。

S(n) = O(f(n))

在交换变量的时候我们通常使用一个临时变量temp存放某个变量的值，这个就是空间复杂度