前排提醒:
阅读本文时记得要动脑子和动笔,不要想当然。
一、反向传播是什么
“反向传播”(Backpropagation) 是深度学习中训练神经网络的核心算法
神经网络训练时,从损失函数(最终误差)出发,沿着神经网络的层反向计算每个参数的梯度,并利用梯度下降法更新参数,最终让损失函数变小(模型预测更准)的过程。
前向传播:“输入数据→经过各层计算→输出预测值→计算损失(误差)”(从输入到输出);
反向传播:“从损失出发→反向算出每一层参数该怎么调整→更新参数”(从输出回到输入);
一般而言,需要做一次前向传播才能做一次反向传播。
核心目的:求参数的梯度
神经网络的参数(权重 W、偏置 b)需要不断调整,而调整的依据是梯度(参数变化对损失的影响程度)。
反向传播的本质就是用链式法则(微积分里的复合函数求导),把 “损失对最终输出的梯度” 一步步传递回每一层,算出 “损失对每一个参数的梯度”。
二、结合ReLu函数
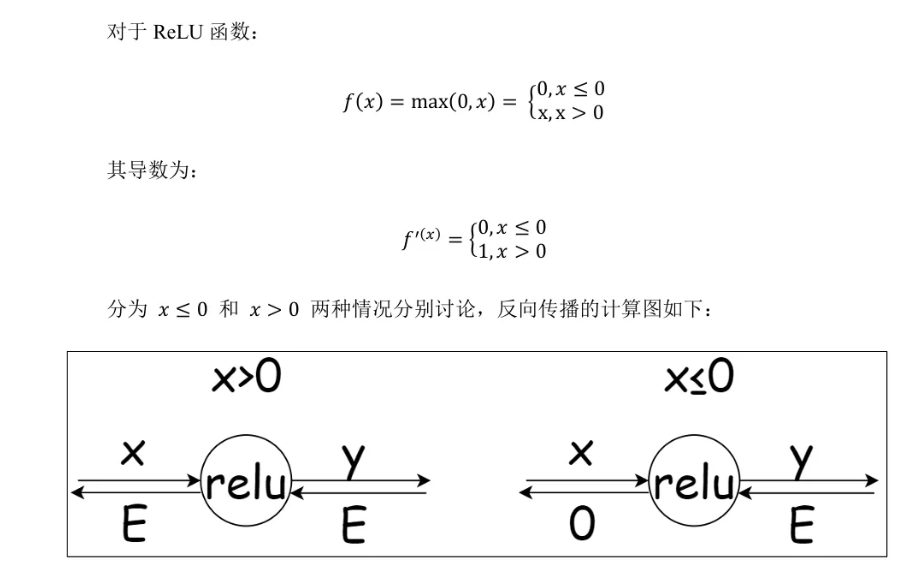
假设我们有一个极简网络:输入x → 全连接层(W,b) → ReLU层 → 输出y → 损失L
步骤 1:前向传播(正向算结果)
全连接层:z = x*W + b
ReLU 层:y = max(z, 0)(就是我们写的 ReLU.forward)
损失:L = (y - 真实值)²(比如均方误差损失)
步骤 2:反向传播(反向算梯度)
我们的目标是算dL/dW(损失对权重 W 的梯度)和dL/db(损失对偏置 b 的梯度),用链式法则拆解:
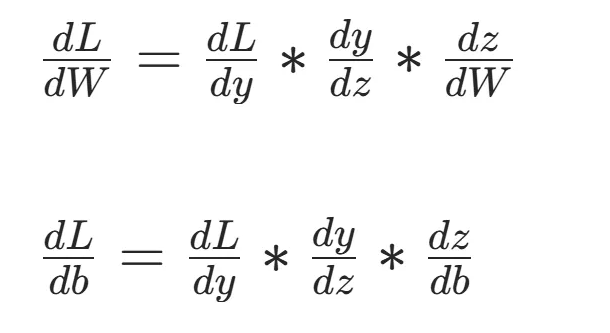
最终,反向传播就是把这些梯度 “从后往前” 乘起来,得到每个参数的梯度,再用W = W - 学习率*dL/dW更新参数。
逐个拆解(结合 ReLU 类):
dL/dy:损失对 ReLU 输出 y 的梯度(比如L=(y-t)²,则dL/dy=2*(y-t));dy/dz:ReLU 的导数(z>0 时 = 1,z≤0 时 = 0)—— 这就是后续 ReLU.backward 里用mask清零梯度的逻辑;dz/dW:全连接层对 W 的导数(=x),dz/db=1;
最终,反向传播就是把这些梯度 “从后往前” 乘起来,得到每个参数的梯度,再用W = W - 学习率*dL/dW更新参数。
结合我们写的 ReLU.backward 理解
我们的 ReLU 类的backward函数,就是反向传播中 “ReLU 层” 的梯度计算步骤:
- 输入
dout:其实就是dL/dy(损失对 ReLU 输出的梯度); dout[self.mask] = 0:就是计算dy/dz * dout(因为 z≤0 时dy/dz=0,所以梯度清零;z>0 时dy/dz=1,梯度不变);- 返回的
dx:就是dL/dz(损失对 ReLU 输入 z 的梯度),会传递给前一层(全连接层)继续反向计算。
反向传播的关键特点
- 链式法则是核心:把复杂的复合函数求导拆解成多个简单导数的乘积,从后往前逐层计算;
- 效率高:一次反向传播就能算出所有参数的梯度,不用重复计算;
- 和前向传播配套:前向传播时会记录中间结果(比如 ReLU 的
mask),反向传播时复用这些结果快速算梯度。
三、具体简单案例
指定的数值(x=2、W=3、b=1、真实值 = 5),搭建一个极简神经网络(输入→全连接层→ReLU 层→损失)
第一步:先明确网络结构
我们的极简网络只有 3 层:
输入x → 全连接层(W=3, b=1)→ ReLU层 → 输出y → 损失L(均方误差)- 全连接层公式:z=x∗W+b
- ReLU 层公式:y=max(z,0)
- 损失函数(均方误差):L=1/2(y−t)2(加 1/2 是为了求导时消去系数,不影响梯度方向)
第二步:前向传播(正向算结果)
我们从输入 x 开始,一步步算到损失 L:
| 步骤 | 公式 | 数值计算 | 结果 |
|---|---|---|---|
| 1. 全连接层计算 | z=x∗W+b | z=2∗3+1=7 | z=7 |
| 2. ReLU 层计算 | y=max(z,0) | y=max(7,0)=7 | y=7 |
| 3. 损失计算 | L=1/2(y−t)2 | L=1/2(7−5)2=1/2∗4=2 | L=2 |
前向传播结论:输入 x=2 经过网络后输出 y=7,和真实值 5 的损失是 2。
第三步:反向传播(反向算梯度)
反向传播的核心是链式法则,从损失 L 出发,反向算每一层的梯度,最终得到损失对 W、b、x 的梯度(我们的目标是更新 W 和 b)。
先明确反向传播的目标
我们需要算 3 个梯度:
- dL/dy:损失对 ReLU 输出 y 的梯度
- dL/dz:损失对全连接层输出 z 的梯度(ReLU 的输入)
- dL/dW、dL/db:损失对全连接层参数 W、b 的梯度(最终要用来更新参数)
逐步骤计算梯度(纯数值)
步骤 1:计算dL/dy(损失对 ReLU 输出 y 的梯度)
- 公式:dL/dy=dyd[1/2(y−t)2]=y−t
- 数值计算:dL/dy=7−5=2
- 结论:dL/dy=2
步骤 2:计算dL/dz(损失对全连接层 z 的梯度,对应 ReLU 反向)
ReLU 的导数规则:
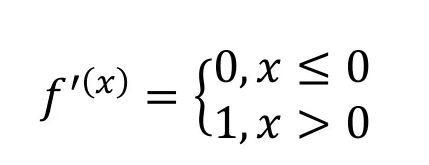
根据链式法则:dL/dz=dL/dy∗dy/dz
- 先判断 z 的取值:z=7>0 → dy/dz=1
- 数值计算:dL/dz=2∗1=2
- 结论:dL/dz=2(这一步对应我们 ReLU 类的 backward 函数:因为 z>0,mask 为 False,所以 dout 不变,直接返回 2)
步骤 3:计算dL/dW(损失对权重 W 的梯度)
全连接层 z 对 W 的导数:dz/dW=x根据链式法则:dL/dW=dL/dz∗dz/dW
- 数值计算:dL/dW=2∗2=4
- 结论:dL/dW=4(W 的梯度是 4,更新时 W 要减去 “学习率 ×4”)
步骤 4:计算dL/db(损失对偏置 b 的梯度)
全连接层 z 对 b 的导数:dz/db=1根据链式法则:dL/db=dL/dz∗dz/db
- 数值计算:dL/db=2∗1=2
- 结论:dL/db=2(b 的梯度是 2,更新时 b 要减去 “学习率 ×2”)
额外:计算dL/dx(损失对输入 x 的梯度)
全连接层 z 对 x 的导数:dz/dx=W根据链式法则:dL/dx=dL/dz∗dz/dx
- 数值计算:dL/dx=2∗3=6
- 结论:dL/dx=6
第四步:梯度更新示例(验证逻辑)
假设学习率 η=0.1(超参数,控制更新幅度),更新 W 和 b:
- 新 W = 原 W - η×dL/dW = 3 - 0.1×4 = 2.6
- 新 b = 原 b - η×dL/db = 1 - 0.1×2 = 0.8
更新后再做一次前向传播:
- z = 2×2.6 + 0.8 = 6
- y = max(6, 0) = 6
- L = 1/2×(6-5)² = 0.5
可以看到:损失从 2 降到了 0.5,说明参数更新有效。
总结(核心数值)
| 梯度名称 | 公式 | 数值结果 |
|---|---|---|
| dL/dy | y - t | 2 |
| dL/dz | dL/dy × dy/dz | 2 |
| dL/dW | dL/dz × x | 4 |
| dL/db | dL/dz × 1 | 2 |
| dL/dx | dL/dz × W | 6 |
这个过程完美对应我们后续写的 ReLU 类:
- 前向传播:z=7>0 → ReLU 输出 y=7(mask=False,无位置置 0);
- 反向传播:dout=dL/dy=2 → 因为 mask=False,所以 dx=dout=2(即 dL/dz=2)。
四、代码示例
import numpy as np # 导入numpy,支持数组的布尔索引、copy等操作
class Relu:
"""
基于NumPy实现的ReLU激活层类
核心功能:
- 前向传播:y = max(x, 0),记录x<=0的位置
- 反向传播:根据记录的位置清零梯度(ReLU导数特性)
"""
def __init__(self):
# 初始化mask,用于标记前向传播中x<=0的位置(布尔数组)
self.mask = None
def forward(self, x):
"""
ReLU前向传播计算
参数:
x (np.ndarray): 输入数组(神经网络前一层输出)
返回:
np.ndarray: ReLU激活后的输出(x>0保留,x<=0置0)
"""
# 生成布尔掩码:x<=0的位置为True,x>0为False
self.mask = (x <= 0)
# 复制输入避免修改原数据
out = x.copy()
# 把mask为True的位置置0(实现ReLU核心逻辑)
out[self.mask] = 0
return out
def backward(self, dout):
"""
ReLU反向传播计算梯度
参数:
dout (np.ndarray): 后一层传递过来的输出梯度
返回:
np.ndarray: 当前层输入的梯度(传递给前一层)
"""
# 利用mask清零x<=0位置的梯度(对应ReLU导数为0)
dout[self.mask] = 0
# x>0位置梯度不变(对应ReLU导数为1),直接赋值
dx = dout
return dx
# 测试代码(仅在直接运行该文件时执行)
if __name__ == "__main__":
# 1. 创建ReLU实例
relu = Relu()
# 2. 前向传播测试
x = np.array([3.0, -2.0, 0.0, 5.0, -1.5])
out_forward = relu.forward(x)
print("前向传播输出:", out_forward) # 预期输出:[3. 0. 0. 5. 0. ]
# 3. 反向传播测试
dout = np.array([0.5, 1.2, 0.8, 0.3, 0.7])
dx_backward = relu.backward(dout)
print("反向传播梯度:", dx_backward) # 预期输出:[0.5 0. 0. 0.3 0. ]