一、引入

交叉熵误差常用于多分类问题

模型的输出 y：让模型认为图片是各种类别的可能性。例如，[0.1, 0.2, 0.7] 可能代表模型认为这张图有 10% 的概率是猫，20% 的概率是狗，70% 的概率是马

真实的标签 t：是一个 “标准答案”。例如，如果图片其实是 “狗”，那么标准答案就是 [0, 1, 0]（叫做one-hot 编码），或者直接是数字 1（这叫做类别标签）

交叉熵误差就是一个 “打分” 工具，它用来衡量模型的预测结果 y 和标准答案 t 之间的差距有多大

若差距越大，说明模型错得越离谱，交叉熵误差的值就越大

若差距越小，说明模型预测得越准，交叉熵误差的值就越小

训练模型的最终目标，就是通过调整内部参数，让这个交叉熵误差变得尽可能小

二、公式原型

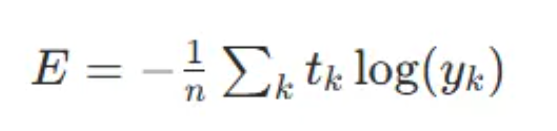
在此说明：

n：样本的数量

k：类别的索引（比如第 1 类、第 2 类...）

y_k：模型预测为第 k 类的概率

t_k：真实标签中第 k 类的值

如果真实标签 t 是 one-hot 编码的（比如 [0, 1, 0]），那么 t_k 中只有一个元素是 1，其他都是 0。所以，求和符号 ∑ 实际上只剩下了真实类别那一项

假设真实类别是第 2 个（索引为 1，索引按照0，1，2，3....排序），那么公式就变成了：E = -log(y1)

三、代码实例

# 交叉熵误差
def cross_entropy(y, t):
    # 将y转为二维
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
    # 将t转换为顺序编码（类别标签）
    if t.size == y.size:
        t = t.argmax(axis=1)
    n = y.shape[0]
    return -np.sum( np.log(y[np.arange(n), t] + 1e-10) ) / n

第一步：定义一个名为 cross_entropy 的函数，它接收两个参数：

y：模型的输出（预测概率）

t：真实的标签

# 交叉熵误差
def cross_entropy(y, t):

第二步：统一数据格式

y.ndim 是获取 y 的维度。ndim == 1 表示 y 是一个一维数组，比如 [0.1, 0.2, 0.7]

为了让代码能够处理多个样本（例如，一个批次的数据），我们希望 y 和 t 都是二维数组。第一维是样本数量，第二维是每个样本的类别概率或标签

reshape(1, t.size) 的作用就是把一个一维数组 [a, b, c] 变成一个二维数组 [[a, b, c]]

    # 将y转为二维
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

第三步：统一标签格式

t.size == y.size 这个条件判断是用来检测 t 是否是 one-hot 编码。比如 y 是 [[0.1, 0.2, 0.7]]，t 是 [[0, 1, 0]]，它们的元素总数是相等的

如果 t 是 one-hot 编码，我们就需要把它转换成类别标签（一个数字）

t.argmax(axis=1) 就是用来找最大值所在位置的

• axis=1 表示沿着每一行（也就是每个样本）去寻找
• 对于 t = [[0, 1, 0]]，最大值 1 在第 1 个位置（索引从 0 开始），所以 argmax 的结果就是 [1]

这样做的好处是：无论你输入的标签 t 是 one-hot 编码 [[0, 1, 0]] 还是类别标签 [1]，经过这一步处理后，t 都会变成统一的类别标签格式 [1]

# 将t转换为顺序编码（类别标签）
    if t.size == y.size:
        t = t.argmax(axis=1)

第四步：获取样本的数量

y.shape 会返回一个元组，表示数组的维度。对于二维数组 y，y.shape[0] 就是第一维的大小，也就是样本的数量 n

n = y.shape[0]

第五步：计算核心部分

np.arange(n): 生成一个从 0 到 n-1 的数组。如果 n=3，它就生成 [0, 1, 2]。这代表了所有样本的索引

y[np.arange(n), t]: 这是一个非常巧妙的索引方式，叫做 “花式索引”

• 它的作用是：对于第 i 个样本（i 从 np.arange(n) 中来），我们从 y 中取出它在 t[i] 类别上的概率

• 举例：

  • 假设 n=2（有 2 个样本），y = [[0.1, 0.8, 0.1], [0.7, 0.2, 0.1]]
  • t = [1, 0]（第一个样本的真实类别是 1，第二个是 0）
  • np.arange(2) 是 [0, 1]
  • y[[0, 1], [1, 0]] 就会取出 y[0, 1] 和 y[1, 0]
  • 所以结果是 [0.8, 0.7]。这正是我们想要的：每个样本在其真实类别上的预测概率

+ 1e-10: 这是一个非常重要的数值稳定性技巧。

• np.log(0) 的结果是负无穷大 (-inf)，这在计算机计算中是一个无效值，会导致后续计算出错
• 为了防止模型预测的概率 y 恰好为 0，我们给它加上一个非常非常小的数 1e-10（0.0000000001），这样 np.log 就不会出错了

np.log(...): 对取出的概率值取自然对数

np.sum(...): 将所有样本的 log 值加起来

- ...: 根据公式，在总和前面加上负号

... / n: 最后除以样本总数 n，得到所有样本的平均交叉熵误差

return -np.sum( np.log(y[np.arange(n), t] + 1e-10) ) / n

总结

这个函数的完整工作流程是：

1. 输入处理：检查 y 和 t 的维度和格式
2. 统一格式：
3. 如果 y 是一维的，就把它和 t 都变成二维的
4. 如果 t 是 one-hot 编码，就把它转换成类别标签
5. 核心计算：
6. 使用 “花式索引” y[np.arange(n), t] 高效地取出每个样本在其真实类别上的预测概率
7. 加上一个极小值 1e-10 防止 log(0) 错误
8. 对这些概率值取对数、求和、取负、再求平均
9. 返回结果：返回最终计算出的平均交叉熵误差